Back

Data structures

Simply put, a data structure is a container that stores data in a specific layout. This “layout” allows a data structure to be efficient in some operations and inefficient in others. Your goal is to understand data structures so that you can pick the data structure that’s most optimal for the problem at hand.

Data structure is a collection of values and algorithms are the steps or processes we put into place to manipulate these collection of values. It’s what allows us to write programs.

A person who knows how data structures and algorithms and how to use them, can write programs great programs.

No matter what problem are you solving, in one way or another you have to deal with data — whether it’s an employee’s salary, stock prices, a grocery list, or even a simple telephone directory.

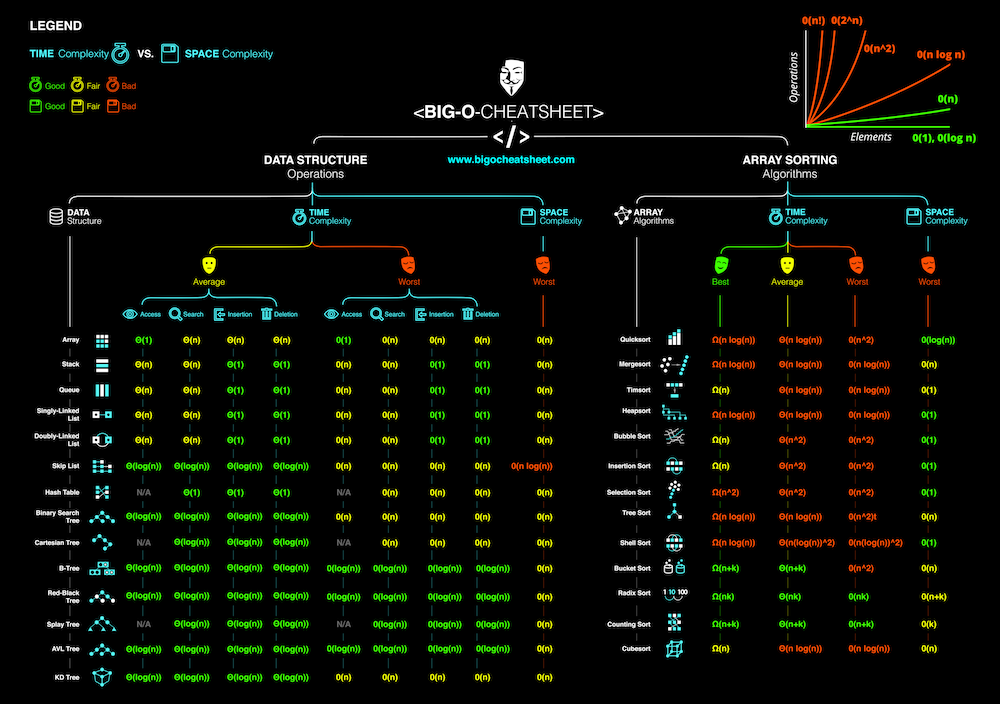
The most used data structures

The values in a data structure can have relationships among them and they can have functions applied to them. Each one is different in what it can do and what it is best used for.

The most important thing to take away is that each data structure is good and is specialized for its own thing.

There are two parts to understanding Data Structures

The second part is usually most importante, because data structure are usually just tools and most of the time they are already pre-built for us.

Each data structure has their tradeoffs, some are good at certain operations and others are good at other operations.

Big-O Cheat Sheet Poster

Big-O Cheat Sheet

Computer memory

Given that we are always going to store our data on a computer, it makes sense for us to find out a little bit about how that information is stored.

Things like variables, numbers, or arrays are stored in what we call random access memory or RAM for short. In RAM you lose the memory when the computer turns off. However, RAM is faster than the hard drive.

RAM

RAM2

Bits, bytes, and words

The most fundamental unit of computer memory is the bit, it can only take one of two values: it is either “on” or “off”.

A collection of 8 bits is called a byte and (on the majority of computers today) a collection of 4 bytes, or 32 bits, is called a word. At the lowest level, any data stored on a computer is just a large collection of bits, a data set is just a series of zeroes and ones.

The number of bytes and words used for an individual data value will vary depending on the storage format, the operating system, and even the computer hardware, but in many cases, a single letter or character of text takes up one byte and an integer, or whole number, takes up one word. A real or decimal number takes up one or two words depending on how it is stored.

For example, the text “hello” would take up 5 bytes of storage, one per character. The text “12345” would also require 5 bytes. The integer 12,345 would take up 4 bytes (1 word), as would the integers 1 and 12,345,678. The real number 123.45 would take up 4 or 8 bytes, as would the values 0.00012345 and 12345000.0.

Bits, bytes, and words

Binary, Octal, and Hexadecimal

Binary

A piece of computer memory can be represented by a series of 0’s and 1’s, with one digit for each bit of memory; the value 1 represents an “on” bit and a 0 represents an “off” bit. This notation is described as binary form. For example, below is a single byte of memory that contains the letter ‘A’ (ASCII code 65; binary 1000001).

Octal

A single word of memory contains 32 bits, so it requires 32 digits to represent a word in binary form. A more convenient notation is octal, where each digit represents a value from 0 to 7. Each octal digit is the equivalent of 3 binary digits, so a byte of memory can be represented by 3 octal digits.

Binary values are pretty easy to spot, but octal values are much harder to distinguish from normal decimal values, so when writing octal values, it is common to precede the digits by a special character, such as a leading ‘0’.

As an example of octal form, the binary code for the character ‘A’ splits into triplets of binary digits (from the right) like this: 01 000 001. So the octal digits are 101, commonly written 0101 to emphasize the fact that these are octal digits.

Hexadecimal

An even more efficient way to represent memory is hexadecimal form. Here, each digit represents a value between 0 and 16, with values greater than 9 replaced with the characters a to f. A single hexadecimal digit corresponds to 4 bits, so each byte of memory requires only 2 hexadecimal digits. As with octal, it is common to precede hexdecimal digits with a special character, e.g., 0x or #. The binary form for the character ‘A’ splits into two quadruplets: 0100 0001. The hexadecimal digits are 41, commonly written 0x41 or #41.

Another standard practice is to write hexadecimal representations as pairs of digits, corresponding to a single byte, separated by spaces. For example, the memory storage for the text “just testing” (12 bytes) could be represented as follows:

6a 75 73 74 20 74 65 73 74 69 6e 67

When displaying a block of computer memory, another standard practice is to present three columns of information: the left column presents an offset, a number indicating which byte is shown first on the row; the middle column shows the actual memory contents, typically in hexadecimal form; and the right column shows an interpretation of the memory contents (either characters, or numeric values). For example, the test “just testing” is shown below complete with offset and character display columns.

0 : 6a 75 73 74 20 74 65 73 74 69 6e 67 just testing

References

Data structures